简介
Fenwick Tree 又叫二分索引树(Binary Index Tree),是一种树状结构的数组。该数据结构是由 Peter M. Fenwick 在1994年首次提出来的。最初,Fenwick Tree 被设计用于数据压缩,而现今,该数据结构主要用来存储频次信息或者用于计算累计频次表等。
对于普通的数组,更新数组中的某一元素需要O(1)的时间,计算数组的第n项前缀和(即前n项和)需要O(n)的时间。而 Fenwick Tree 可以在O(log n)的时间内更新结点元素,在O(log n)的时间内计算前缀和。
结构
要介绍 Fenwick Tree 的结构,我们首先来介绍一个函数lowbit(x)。lowbit(x)函数返回x的二进制表示最右位1所代表的值。例如,1232的二进制为0100 1101 0000,其最右位1所代表的值为二进制10000即\(2^4=16\),那么lowbit(1232)=16。
在计算机中,lowbit(x)计算方式如下:
int lowbit(int x) {
return x & -x;
}我们来看一下 Fenwick Tree 的结构:横坐标是x,代表数组的下标;纵坐标是lowbit(x)。
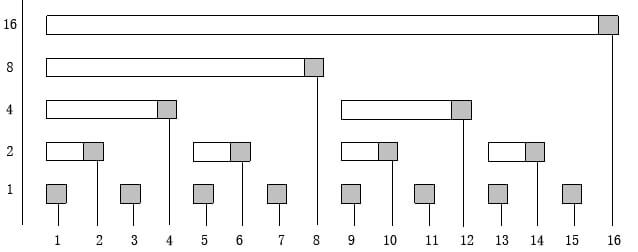
在上图中,长条代表树状数组中的每一个结点的求和范围,x对应长条的长度为lowbit(x),也就是说,下标x的树状数组结点表示范围为[x - lowbit(x) + 1, x]的原数组之和。
我们用arr表示一个普通数组,用tree表示与之对应的树状数组,则有
$$\texttt{tree[x]}=\sum_{i=x-lowbit(x)+1}^{x} \texttt{arr[i]}$$
由图可以看出,对于节点x:
- 其左上相邻结点为
x - lowbit(x) - 其右上相邻结点为
x + lowbit(x)
操作
求前x项和
若要计算前x项和,则从x向左走,边走边往上爬,则经过的所有长条不重复不遗漏地包括了所有需要累加的元素。
实现代码如下:
int sum(int x) {
int ans = 0;
while(x > 0) {
ans += tree[x];
x -= lowbit(x);
}
return ans;
}更新第x项
若要更新第x项,则从x向右走,边走边往上爬,沿途修改所有经过的结点即可。
实现代码如下:
void add(int x, int val) {
while(x <= N) {
tree[x] += val;
x += lowbit(x);
}
}获取第x项的值
要获得第x项的值,可以直接用sum(x) - sum(x - 1)来计算。考虑到sum(x)和sum(x - 1)在计算过程中有相同的部分,相减会被抵消。因此,我们只需要计算sum(x)和sum(x - 1)不同部分之差即可。
实现代码如下:
int get(int x) {
int ans = tree[x];
if (x > 0) {
int z = x - lowbit(x);
x--;
while(x != z) {
sum -= tree[x];
x -= lowbit(x);
}
}
return ans;
}Python 实现代码
class FenwickTree(object):
def __init__(self, n):
self.sum_array = [0] * (n + 1)
self.n = n
def lowbit(self, x):
return x & -x
def add(self, x, val):
while x <= self.n:
self.sum_array[x] += val
x += self.lowbit(x)
def sum(self, x):
ans = 0
while x > 0:
ans += self.sum_array[x]
x -= self.lowbit(x)
return ans
def get(self, x):
ans = self.sum_array[x]
if x > 0:
z = x - self.lowbit(x)
x -= 1
while x != z:
ans -= self.sum_array[x]
x -= self.lowbit(x)
return ans